ECC 杂谈：NIST / NSA 后门，Curve25519

最近由于工作原因，接触了不少现代计算机密码学知识。想写点东西分享分享，但由于学的都是些皮毛，属于将就能够应用的水平，这里只能写一篇杂谈，闲聊下 ECC 和 25519。

ECC 简介

#

现代计算机的安全性离不开公钥密码学，而公钥密码学的基础构建在数学之上。与较为出名的 RSA 加密系统的算法建立在分解两个大素数乘积（因式分解）的困难性上不同，椭圆曲线密码学 Elliptic-curve cryptography，即 ECC，是建立在求解椭圆曲线离散对数问题的困难度上。其显著的特点是，对比 RSA 来说 ECC 实现同等加密强度所需的密钥长度要小很多，并且所需的算力开销也更小。

基于 ECC 的具体应用主要分布在两方面：

• 数字签名 – 被广泛应用在身份认证、完整性检查等领域
• 密钥协商 – 用于现代加密通信最关键的部分：在不可信的信道上进行加密密钥的协商

而目前世界上较为流行的 ECC 标准又可大致分为两类：

• 由 NIST (美国国家标准与技术研究院) 推荐的多个曲线，定义在 2000 年发布的 FIPS 186-2 中
• 由世界著名的密码学家 Daniel J. Bernstein 在 2006 年发布的 25519 曲线

由于较早推出，NIST 的曲线得到了广泛的应用。如数字签名算法 ECDSA 在 X509 证书标准中的使用，生产出的对象即是现如今正逐步普及的 ECC 证书。

而在像 OpenSSL 等一众开源 TLS 实现中，NIST 的曲线在密钥协商 ECDH 中更是被作为优先选择。

在很长的一段时间内，NIST Curve P-256 是 OpenSSL ECDH 默认曲线列表中的首选。

OpenSSL 代码中虽然没有注释说明是 NIST 标准，我们可以自行对 P-256 的 P 简单做个换算看看 Hex 是否一致。

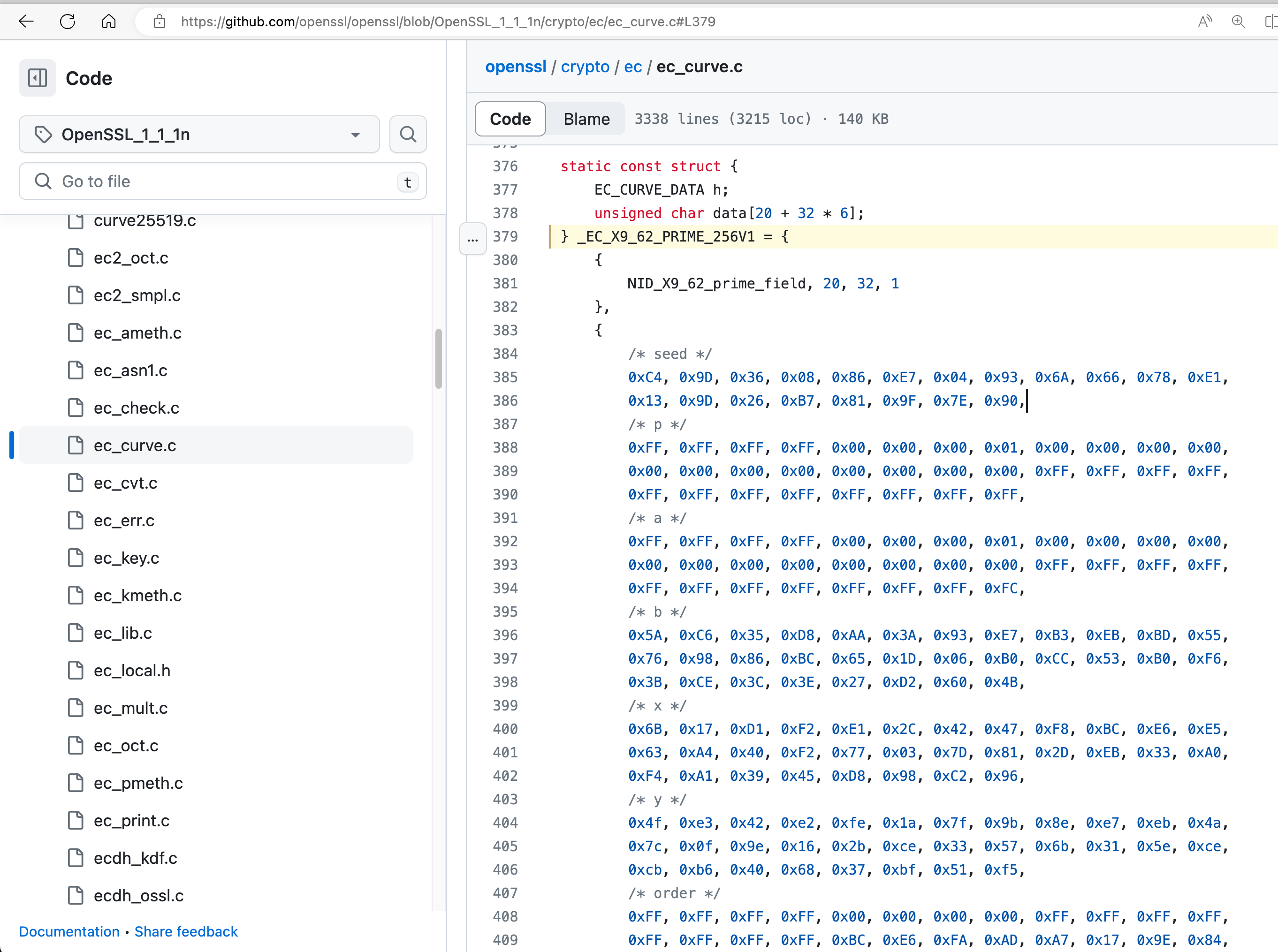
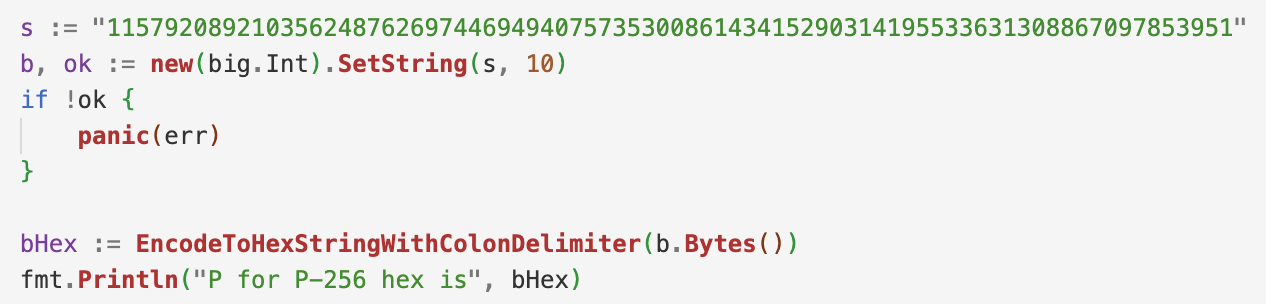
可以发现确实是 NIST 的曲线无疑。

可疑的 NIST 椭圆曲线，NSA 的后门劣迹

#

从上面 OpenSSL 的代码截图中可以看见，NIST 的 P-256 曲线被叫做 PRIME_256V1. 这个名字其实来自于 1998 年的 ANSI X9.62 ECDSA 规范，至于为什么 NIST 的曲线参数跟这个 ANSI 规范的一模一样，是因为后来的 NIST 直接使用了这些曲线。那么问题是，这些曲线为何这样定义？它们又是哪里来的？这两个问题至今没有清晰的答案。因为现实就是这些曲线中的 Seed 定义既没有解释或理由，也没有任何连来历信息。但是在各种密码学、计算机圈子内都倾向于一个统一的，合理的猜测 – 它们是来自于 NSA（美国国家安全局）。

那么，更为重要的灵魂问题是: 它们是否存在弱点或后门？

如果说从这些曲线发布的那天起，对其的质疑 ¹ 只在小范围专业圈子内传播，到了 2013 年 9 月 6 日在纽约时报网络版上的一篇新闻 ² 披露出的内容则是在公共领域掀起了轩然大波：根据 爱德华·斯诺登（对，就是棱镜门的主角）披露的机密文件显示，NSA 曾经向某密码学算法植入后门并将其通过 NIST 确立为国家标准。虽然文内并未直接披露是什么算法，但却隐晦的描述了这样的一段话：

Classified N.S.A. memos appear to confirm that the fatal weakness, discovered by two Microsoft cryptographers in 2007, was engineered by the agency. The N.S.A. wrote the standard and aggressively pushed it on the international group, privately calling the effort “a challenge in finesse.”

这让业界很快就锁定到了具体的对象，就是早在 2007 年就由两名来自微软的密码学研究专家发现可以被植入后门 ³ 的伪随机数生成算法：来自 NIST SP800-90 的 Dual_EC_DRBG.

紧接着在同年的 12 月，路透社更是直接独家爆料出了 NSA 对 RSA 公司进行 $10 million 的贿赂，将 Dual_EC_DRBG 作为 RSA 商业产品 Bsafe 中首选的随机数生成算法的事 ⁴。

很快，越来越多的证据都指出 Dual_EC_DRBG 确实存在可能的后门 ^{5 6}，工业界纷纷开始抛弃 Dual_EC_DRBG，并且随之而来的还有愈演愈烈的对 NIST 曲线的质疑 ^{7 8 9}，可以说从 2013 后，密码学进入了 「后斯诺登时代」，业界急需一个透明、公开、可审查、可持续改进的 ECC 实现来摆脱 NSA 这个"美国老大哥"给出的可疑曲线。

Curve25519，X25519，Ed25519

#

随着业界对 NIST 椭圆曲线的不信任加剧，原先于 2006 年发布后只在学术界传播的 25519 曲线热度迅速提升，各工业界的软件开始纷纷加入对 25519 曲线的支持。一方面是信任问题，另一方面是 ECC 在工业界使用上存在可能的专利纠纷 ¹⁰，而 Curve25519 是公共领域的产物，不受任何专利保护 ¹¹。

RFC 在 2016 年 1 月 推出的 RFC 7748 明确了在 ECDH 协议中应用 25519 曲线的 X25519 方法，而 Ed25519 则是出现在 2017 年 1 月的 RFC 8032 这个对 EdDSA 数字签名算法进行了更加明晰的标准化规范中，可以说自此之后，可疑的 NIST 曲线将会逐步的退出历史舞台。

从理论上说，25519 曲线的优势在于：

• 没有专利约束

• 公开，透明的参数，可信度高 – 不像 NIST 的曲线那样存在可疑的、来路不明的 Seed

• 实用安全性高，力图通过精心设计的实用性做好安全性防护

  理论上的安全性不等于实际上的安全性，因为不恰当的实现导致的漏洞不在少数 – 最著名的例子就是索尼的 PS3 ^{12 13}

  对于曲线的安全性探究可以参考：SafeCurves: choosing safe curves for elliptic-curve cryptography

• 性能优异，计算速度上比 NIST 曲线要快很多，对低算力的硬件更友好

• 公钥长度很短，只有 32 bytes

  按 Go 标准库中给出的算法计算了下，NIST 的各个曲线的公钥长度如下：

  NIST Curve	Public Key Bytes Length
  P-224	57
  P-256	65
  P-384	97
  P-521	133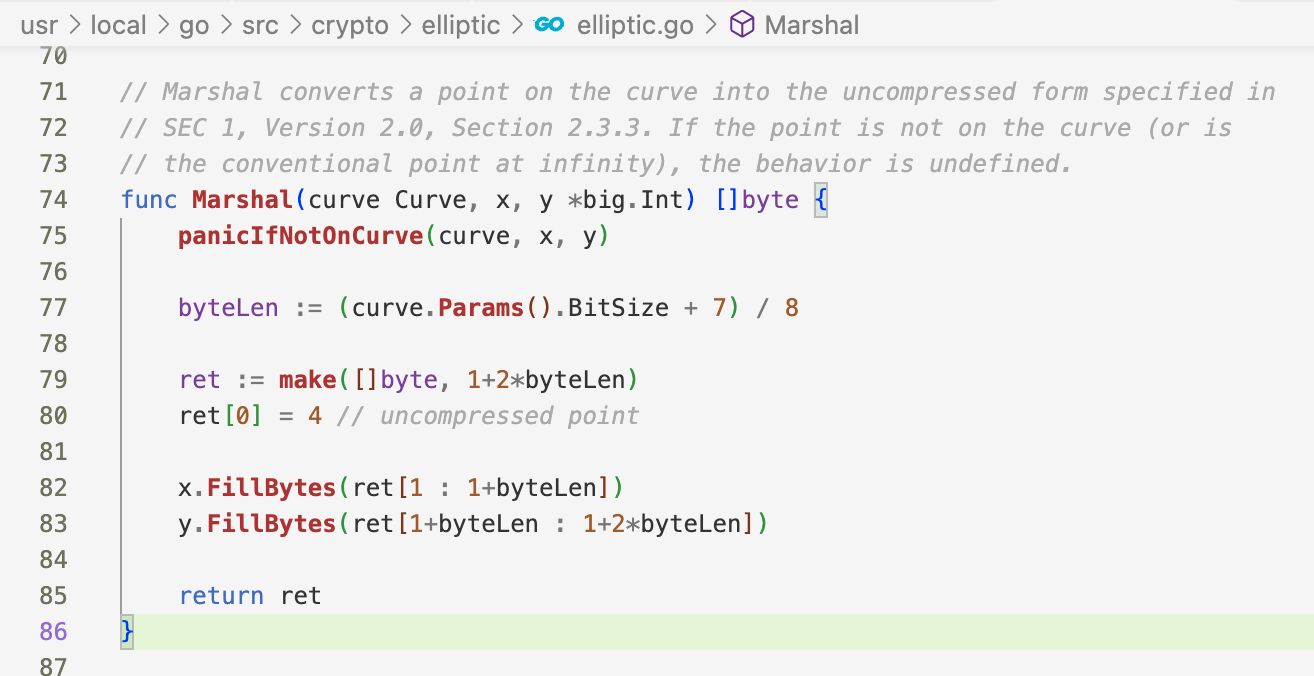

  

  可以看出 25519 这个公钥长度确实比 NIST 的要短很多。

IANIX 专门有一个网页列出了使用 25519 曲线的软件/软件库：Things that use Curve25519，感兴趣的读者可以自行浏览。

下面简单聊聊几个我个人接触较多的使用了 25519 曲线的领域/软件的情况。

OpenSSH 中的 25519

#

SSH 的密钥协商没有看见使用 ECDH 这个术语，而是直接叫 KEX，即 Key Exchange.

OpenSSH 可以通过 ssh -Q kex 查看支持的 KEX 算法

想要知道其他不同的 SSH 实现对 KEX 的支持，可以参考这个矩阵：Key exchange protocols

LibSSH 的 Aris Adamantiadis 于 2013 年 9 月 27 日为 LibSSH 的 KEX 添加了 25591 曲线的支持: kex: implement curve25519-sha256@libssh.org：

是的，就在纽约时报那篇报道之后的同月就完成了，这可能是世界上第一个实现应用 25519 曲线的 SSH 功能库。引用他自己的描述 ¹⁴ 是：

This algorithm does not rely on NIST-based curves and gives us more security confidence against a possible backdoor in nistp-256 curve.

随后这个功能作为 Patch ¹⁵ 被他提交给了 OpenBSD 团队，并且在 2013 年 11 月 3 日进入 OpenBSD 的主线 use curve25519 for default key exchange (curve25519-sha256@libssh.org);：

密钥协商的功能有了，剩下的身份认证那块（Host Key 和 User Authentication Key）对 Ed25519 的支持也在同年的 12 月 完成 support ed25519 keys (hostkeys and user identities) using the public …：

OpenSSH 可以通过 ssh -Q key 查看支持的 Host / User Authentication Key 列表

想要知道其他不同的 SSH 实现对 Host / User Authentication Key 的支持，可以参考这个矩阵: Hostkey formats

所有上述的特性都随着 2014 年 1 月 30 日发布的 OpenSSH 6.5 到来：

OpenBSD 的发布在 5.5，晚了几个月。

上面的两类特性分别在 2020 年的 RFC 8709 和 RFC 8731 被标准化。8709 描述的是如何在 SSH 协议中使用 EdDSA ，8731 则是 KEX 中对 25519 和 448 的使用。

但是我看现在 OpenSSH 也没支持 448 曲线 ¹⁶。

TLS 中的 25519

#

从 IANIX 给出的时间线看，在 RFC 7748 正式发布之前，很多 TLS 相关的软件已经根据 RFC 草案等实现了对 25519 的支持。

看得出搜索巨人 Google 的动作还算比较迅速，毕竟这是出于 Chromium / Chrome 的现实需求。

从发布声明上看，LibreSSL 的实现（2017-02-01，2.5.1）比它那个兄弟 OpenSSL 还要晚接近半年。虽然这可能是因为 LibreSSL 要从 OpenBSD 扣代码导致的，但实际上 OpenBSD 仓库中的实现就是比 OpenSSL 要更晚 ¹⁷。

Libsodium 更晚，在 2017 年 3 月 的 1.0.12 才支持

Golang 中 TLS 标准库对 X25519 的支持是在 2017 年 2 月发布的 1.8 引入的，见 crypto/tls: support X25519 key exchange。比较神奇的是，从这个 issue 中甚至能发现 Google 内部在 2015 年 12 月对 BoringSSL 做测试时使用的是 Go 代码，即当时就已做到用 Go 实现了 X25519。

X509 中的 25519

#

2018 年 8 月发布的 RFC 8410 中正式将 EdDSA 运用在 X509 中，同时也对 RFC 7748 中定义的 X25519 补充了下 ASN.1 的 OID 等信息。可能读者会奇怪：X25519 不是 ECDH 协议使用的算法吗，怎么会有 ASN.1 的定义？原因在于这个 RFC 标准中还有一个比较奇怪的用法: 将 X25519 的公钥签名后放在证书的结构中，所以才需要定义 X25519 的 OID。不过我也没太搞明白具体的用法和意义，网上的资料也相对较少 ¹⁸。

OpenSSL 倒是在同年 9 月 20 日发布的 1.1.1 正式版 ^{19 20} 中支持了 EdDSA 签名的证书，但是截止目前（文章编写时），现实世界中的可信 CA 组织普遍都不支持签发使用 Ed25519 签名方案的证书。